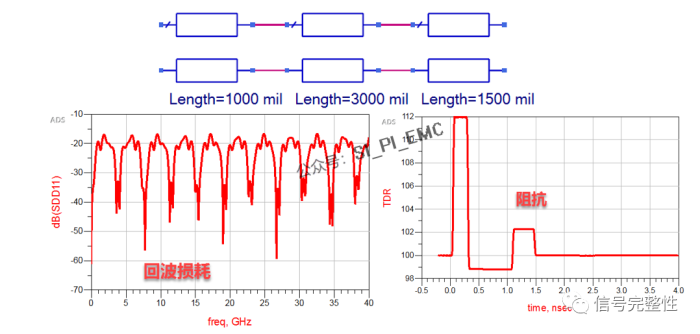
在分析信号完整性和电源完整性问题时经常会提到在时域中分析和在频域中分析。不管是什么分析,分析都是同一个对象。因为有的问题在时域中难以描述,比如能量损失,因为能量是一个系统概念,很难对应到物理对象的点;有的问题则需要在时域中分析,比如时域阻抗。通过傅里叶变换,可以把时域变换到频域;通过傅里叶逆变换,把频域变换到时域。本文只是简单的举例描述时域和频域在分析信号完整性和电源完整性中问题的应用。
时域是真实世界里面存在一个域,描述的是信号与时间的关系;频域则是通过傅里叶变换的数学变换得到的一个域,频域描述的是信号与频率的关系。不管是时域还是频域,分析的对象是相同的,只是分析的角度不同。时域与频域是可以相互转换的。
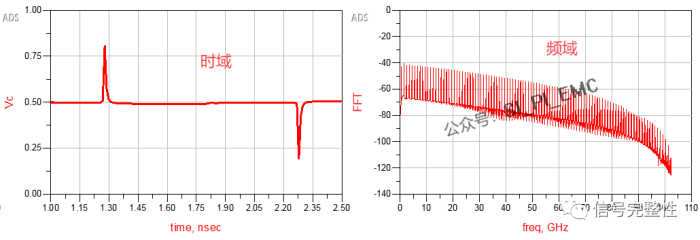
不管是信号完整性还是电源完整性,大家熟悉的肯定都是在时域里面分析。比如下图所示的波形:
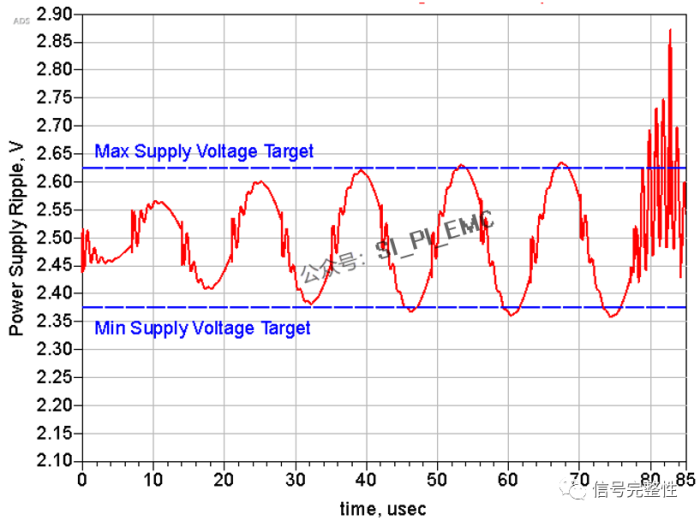
这是一个电源的波形,显然,横坐标是时间轴,纵坐标是电压幅度,每一个时刻对应的电压是多少都非常清楚。这就非常清楚的看出在45us、55us等时间点对应的电源存在问题,其电压超过了小值或大值的要求。那如何解决这个问题呢?通过这个波形结果却并不能直接找到解决问题的方法。这个电源系统对应到的频域曲线如下图所示:
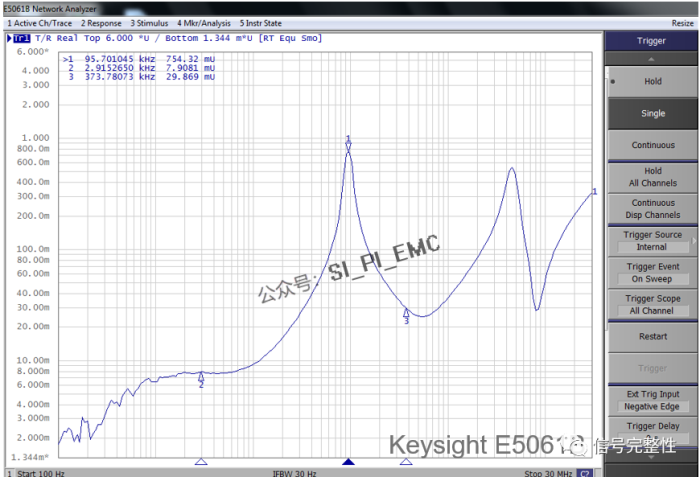
从频域曲线上看到在频率为95.7kHz的幅度比较大,还有其它两个更高频率对应的峰值点。这些峰值点对应的频率可能就是造成电源纹波超标的频率。那如果需要通过电容进行滤波,就可以寻找对应的电容(容值和封装)。
这只是电源完整性中时域和频域应用的一个小场景。如果只是通过时域来分析这个问题,可以看到这个问题的形象,但是通过频域,就可以找到解决这个问题的方法。如前所述,频域是数学构造出来的一个域,科学家或者工程师就可以通过数学方法构造出不同分析问题的函数。在分析信号完整性和电源完整性的时候,需要灵活的运用时域和频域,通过不同的角度来分析信号的干扰、辐射、串扰、损耗以及电源等等问题。这样能更好的解决实际的问题。下图是在时域和频域中分析传输线的特性。