横河示波器的“周期统计功能”，即当被测信号为周期性信号时用户可使用“周期统计”功能，示波器将按照信号周期自动进行测量并输出相关数值。那么当被测波形为非周期性信号时，我们还能使用这一便捷高效的功能对相关参数进行测量统计吗？

一、运算原理

       在讨论FFT低频混淆问题之前，我们先来了解一下采样率和采样定理的概念。采样定理又称奈奎斯特定理，由美国电信工程师H.奈奎斯特在1928年提出。在数字信号处理领域中，采样定理一直都被视为连续时间信号（通常称为“模拟信号”）和离散时间信号（通常称为“数字信号”）之间的基本桥梁。该定理不仅说明了采样频率与信号频谱之间的关系，还是连续信号离散化的基本依据，即在进行模拟/数字信号的转换过程中，当采样频率fs.max大于信号中高频率fmax的2倍 (fs.max>2fmax) 时，采样后的数字信号将完整保留原始信号中的信息，因此在实际应用中我们需要保证采样频率为信号高频率的2.56～4倍。

       对于FFT频谱分析而言：当N个采样点经过FFT变换后即可得到以复数形式所记录下的N个点的FFT结果。假设采样频率为Fs，采样点数为N，那么FFT的运算结果就是N个复数（或N个点），且每一个复数都将对应着一个频率值以及该频率信号的幅值和相位；第一个点对应的频率为0Hz（即直流分量），后一个点N的下一个点所对应的即为采样频率Fs，其中任意一个采样点n所代表的信号频率为：Fn=(n-1)*Fs/N。

       由上述公式可知，经频谱分析后所得的信号频率大为(N-1)*Fs/N，对频率的分辨能力为Fs/N；不难发现在FFT运算过程中，采样频率和采样时间不仅制约着信号频率的上限，同时也限定着经信号频率分析过的分辨率。

二、低频混淆

       鉴于FFT的分析结果具有对称性，且FFT频谱分析频率上限为采样率的一半，因此我们在运算时通常只取用前半部分即小于采样频率一半的结果，毕竟也只有采样频率在一半以内、具有一定幅值的信号频率才是真正的信号频率。也就是说当原始数据的采样率为1Ms/S时，FFT分析频谱的上限即为500KHz。

       看到这里，我们不禁会产生一个疑问“高于频谱分析上限的高频信号难道就不可能出现在FFT的分析结果中吗？”毫无疑问答案是否定的。这里就涉及到FFT频谱分析中信号缺失混淆的问题了。所谓的低频混淆就是当设备在重复波形上通过执行A/D转换进行FFT运算时，超过采样频率一半的频率成分将被识别成低频率成分后所产生的混淆现象。

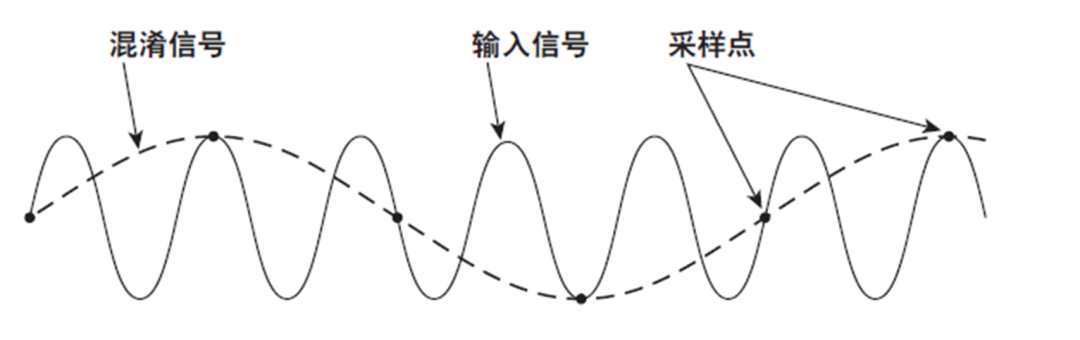
       事实上在FFT分析中，由于用户采样不足，而导致FFT频谱的某个高频点发生偏移后形成错误的FFT频谱图现象时有发生，下面我们来看一个实际案例。实验中所用的原始波形均为由横河示波记录仪采集且经振动传感器转换后的电信号，客户分别使用500Ks/S和1MKs/S做了两次采集，并在记录了同类型信号后使用了Xviewer进行FFT分析：

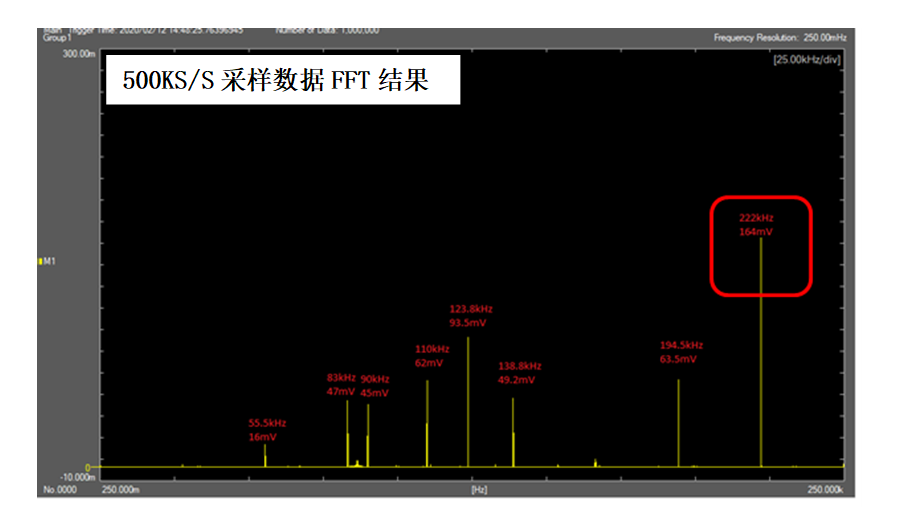
       当我们使用500KS/S的采样波形做FFT分析时，就会发现在222.5KHz频率点出现了一个高频分量（这部分也是客户实际关注的振动频率）。

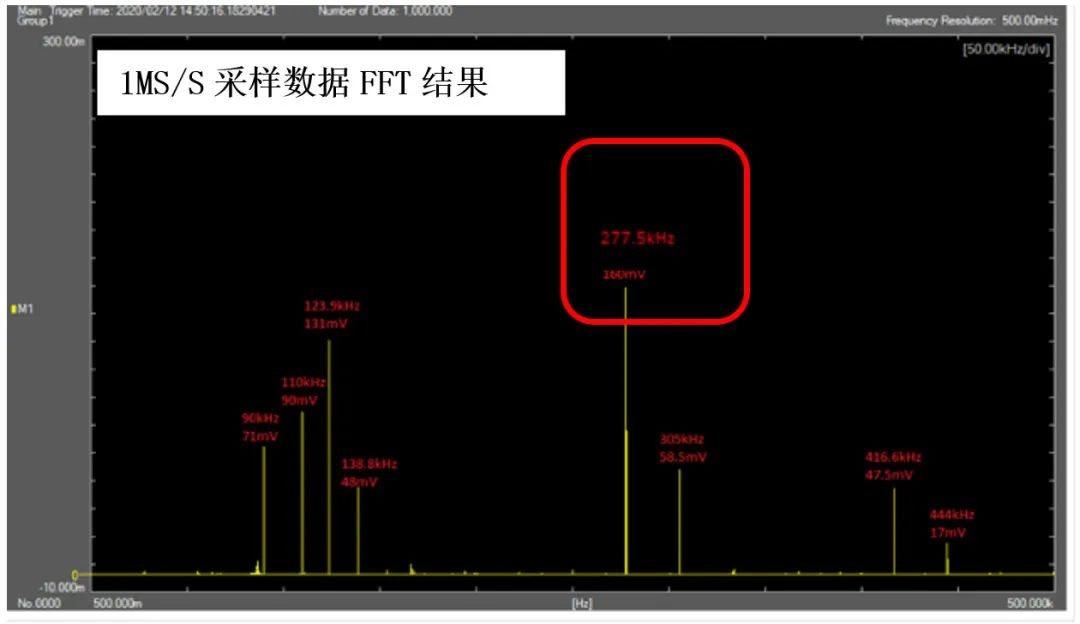
       随后再使用1MS/S的采样数据进行分析，我们可以看到222.5KHz的高频成分消失了，取而代之的则是在277.5KHz处出现了一个频率成分。

       鉴于这个奇异的现象，客户再次使用专业的频谱分析仪进行验证分析，并确认了277.5KHz的成分是正确的，而222.5KHz频点的信号则是由于混淆显现而造成的假数据。也就是说针对该测试信号，由于500KS/S的采样率不足，而引起了250KHz以上的信号混淆到了222.5KHz频点，并形成了错误的FFT频谱分析结果。

       由以上案例可知，当用户在使用示波器/示波记录仪进行波形记录时，采样率不但会影响如上升沿、毛刺等直观的波形细节，还会因欠采样对FFT频谱分析造成完全错误的结果，从而误导工程师们对于产品性能的客观评价。因此，使用FFT频谱分析功能，一定要注意采样率的合理设定。

三、总结

       由以上案例可知，当用户在使用示波器/示波记录仪进行波形记录时，采样率不但会影响如上升沿、毛刺等直观的波形细节，还会因欠采样对FFT频谱分析造成完全错误的结果，从而误导工程师们对于产品性能的客观评价。因此，使用FFT频谱分析功能，一定要注意采样率的合理设定。